2016-09-08

催眠商法（SF商法）潜入ルポ

　昨日12時50分、京■大学近くの某シェアハウスに到着。13時、メ■ーマー■潜入部隊が集合した。作戦は15分後、■都大学から歩いて数分のところに2ヵ月限定で店舗を構える「■リー■■ト」にて決行。ここで行われているのはいわゆる「催眠商法」「SF商法」で、要は来場者プレゼントなどの餌によっておびき寄せた老人・主婦らを心理学的な手法で洗脳し、購買意欲が異常に高まった段階で高価な商品を売りつける悪質な手口だ。
detail.chiebukuro.yahoo.co.jp
　企業名をググってもあまり多くの情報はヒットしないが、2005年にヤフー知恵袋で被害が報告されているのを確認することができる。2ちゃんねるでもたまに言及されるらしい。労働環境が粗悪、脱税が発覚したなんて噂もある。当日0時過ぎにメリ■■■トツアーのことを知ったが、こんなに面白いオモチャもなかなかないのですぐに同行を決めた。

　受付で米1kgを受け取った。入場にはひとりにつき100円が必要となる。すべてが終わったあとにトイレットペーパー12ロールが支給され、さらに前日も参加していれば、メリ■■ー■を紹介した側とされた側がそれぞれティッシュを5箱ずつもらえる。1時間と少し座っていれば確実に1,000円分以上の物資と話のネタが手に入るのならまあ悪くない。
　特に問題なく入場できたが、100人ほどの老人で溢れかえる会場で20代前半の僕たちはとてつもなく浮いた。開始時間の10分以上前にはすでに席が埋まっていたため、最後列に予備の椅子を用意してもらい、着席した。iPhoneのボイスメモを起動してポケットに忍ばせる。内装を撮影しておきたかったが、誰にも気づかれず写真を撮ることはできそうになかった。ただ白いペンキで塗られただけの無機質な壁、古びたパイプ椅子、トイレットペーパーしか並べられていない前方の長机、店長の頭上に掲げられた不気味な笑顔のロゴマーク。見たところ相手方の勢力は3人で、よく喋るガリガリの店長（新婚）、ぽっちゃり体系アラレちゃん眼鏡の女性店員（さーちゃん22歳）、ぎこちない体育会系男性店員。こちらは8人いるので殴り合いになれば奥にあと数人いたとしても勝てるはずだ。

　予定よりも10分ほど早く店長の弾丸セールストークが始まった。

店長「はい、えー、それでは皆様お待たせいたしました！　改めまして、こんにちはー！」
老人「「「こんにちはー！！！」」」
店長「はい、えー、それではですね、まだお時間前ではございますけどもね、あの、ちょっとですね、人が多いんですごく暑いんですけども」
さーちゃん「そうですねー」
店長「あの、今日の朝、もっとすごかったんですよ！」
さーちゃん「はい」
店長「ねえ、あの、けっこうね、お客さんらですね、お昼空いてるからお昼行こうって方が多かったんですね」
さーちゃん「そうですね」
店長「でもですね、朝から少ないかなーと思ったらめちゃめちゃ多くて！　朝も多くてお昼も多くてですね、こんなに街に人がいるのかなと」
さーちゃん「うんー」
店長「噂らしいんですよ。なんかぞろぞろ人が歩いてるけど、祇園祭今日やったかなーって」

　当然だが、喋りはなかなかうまい。老人たちも数日前から複数回ここに来ているため、統率のとれた反応を返してくれる。コールアンドレスポンスもほぼ完璧だ。前日に同じ場面があったのだろう。まるで打ち合わせでもしたかのように声を揃え、老人たちは店長の望んだ通りの反応を引き出される。うまく合わずとも店長がそれを笑いに変え、失敗したところを何度か練習する。おそらくこの練習も後日生かされることになる。僕が店長のジャブにひるんでいると、間髪入れずに店長とさーちゃんのあっちむいてホイバトルが始まった。会場を左右で店長チームとさーちゃんチームに分け、勝った側が全員きしめん1袋をGETする*1。普通に楽しい。この時点でトーク開始から3分。もう引き込まれそうになっている。「こっそり録音している*2」という緊張がなければもうあちら側に取り込まれていたかもしれない。

店長「笑うと人間は免疫が上がります。みなさん、癌という病気、なりたいですかなりたくないですか？　なりたくは？」
老人「「「ない！！！」」」
店長「なりたくは？」
老人「「「ない！！！」」」
店長「（さーちゃんを指差して）彼女はお金が？」
老人「「「ない！！！」」」
店長「そうなんですよー！」
老人「「「ワハハハハハハ！！！」」」

店長「残念ながら健康食品バリバリ食べてる人だけが元気で長生きできるんか言うたらそうでは」
老人「「「ない！！！」」」
店長「そうでは」
老人「「「ない！！！」」」
店長「私は骨と皮しか」
老人「「「ない！！！」」」
店長「いやいやいやいやいや！」
老人「「「ワハハハハハハ！！！」」」

　こんな感じのコールアンドレスポンスが頻繁に挿入され、ちゃんとやらないと体育会系男性店員が圧をかけてくる。彼は背が高いうえに笑顔が下手なので本当に怖い。黙ったまま店長の話を聞いていたら結構マジなトーンで「後ろ2人！」と怒られたし、老人にもたまにきつく当たることがある。さーちゃんより年上とのことだが、濱田マリっぽいハキハキとした喋りのさーちゃんと対照的に店長の話への相槌が絶望的に棒読みで、タイミングもガバガバだ。この仕事をこの先も続けるのなら早く改善したほうがいい。

　店長が健康にかんする話について全然エビデンスを出さないことは少し気になっていたが、序盤はトークのスピードにまんまと誤魔化されていた。疑問を持つ隙も与えてくれない。立ち止まって考えていると店長は先へ先へと話題を変えていってしまう。この話は本当に商品と関係があるのだろうか。だが、20分くらい経った頃に店長がとんでもないことを言い出したもんで、僕はようやく正しく状況を認識することができるところまで回復した。

店長「実はですね、そういう放射能が漏れてですね、魚にですね、大きな影響を与えている魚が、あるんですよ。そしてですね、そういうものを食べるからですね、今ですね、若者たちに、病気がすごく多いんですよ。で、それが何か言うたらみなさん、奇形児とか異常児*3って言われてるんですけども、ねえ、あの、異常児の子供が非常に多い！　もっと言うとですね、あの、異常児じゃなくてもね、アトピー、アレルギーがなんで多いのかって調べてみたときに、親が食べるものが悪過ぎるんですよ！　わかります？　だからですね、今はですね、あの、こういうふうに指が一本少ない子供を少指症*4って言います」
さーちゃん「少指症！（かわいい）」
店長「指が一本少ないんですよね、四本しか無いんですよ。逆にですね、指が一本多い子供を多指症って言うんですよ」
さーちゃん「多指症！（かわいい）」
店長「そしてね、可哀想なのがこの前ですね、海外のほうになるんですけれども、赤ちゃん生まれたら鼻が無かった子供が生まれたんです。鼻が無かった」
さーちゃん＆老人「「「へー！！！」」」
店長「それがですね、あの、なんや言うたら、無い鼻と書いて、無鼻症と呼ばれます！」
男性店員「無鼻症！（棒読み）」
店長「無鼻症！　そしてですね、目が一個しかない子供を、単眼症と言います！」
さーちゃん「単眼症！（かわいい）」
店長「で、単眼症の子供は可哀想にね、目が無いときに、右とか左だけ無いんじゃないんですよ。で、どうなるんですか言うたら目が必ず真ん中に寄るんですね」
老人「「「へー！！！」」」
店長「単眼症って。で、あの、そういう子供が生まれてます。じゃあなんでそういう子供がいま多くなったのか言うたら一番調べてみたら、やっぱり食べ物が悪くなってるんです！」

　店長、お前……よりにもよって理学研究科を置く北部のすぐ近くでやりやがったな……！　僕の頭の中ではなぜか機動戦士ガンダムUCのBGMが流れていた。
　ここで店長は韓国海苔12パックセットの紹介をしたかったようだが、放射能の話は全く必要なかった。「奇形児」「異常児」などの衝撃的なワードで無駄に老人の不安を煽り、なんかよくわからんがとりあえず海苔を買えば安心だというふうにミスリードしたように見えた。

　その後も店長は会場内の学生の目も気にせず根拠の不明瞭な話を続け、さーちゃんはキュートで、体育会系男性店員は棒読みだった。男性店員の発する圧で1時間の洗脳トークは異常に長く感じられた。今日販売された商品はほぼ常識的な価格設定だったが、2ヵ月かけてこの老人たちは徐々に高い商品を買わされるようになっていくことだろう。なんと今だけ12,900円分の青汁を購入するだけで会員登録できるだなんて謳っていたが、もはや誰もおかしいと感じていない様子だった。
　14時半ごろにようやく店長のトークと商品の販売が終了し、僕たちはトイレットペーパーとティッシュを受け取った。人数が人数だけに、なかなかの収穫だ。

f:id:fukuso_sutaro:20160908230705j:plain

　帰り際に潜入部隊のメンバー数人が店長と少し会話した。店長は傍目から見ると来場者プレゼント乞食の僕たちにも優しく対応してくれた。根はいい人なのかもしれない。店長、あんたとはもっと別の出会い方をしたかったよ。そしたら、友達になれたかもしれないな。

　――ある程度の覚悟はしていたが、やはり催眠商法は恐ろしい。年老いた自分がもしひとりだけでこういった場に足を運んでしまったら、正直なところ催眠商法に絶対引っ掛からないとは言えない。今回潜入した8人は、心理学とか社会学とか、何かしらそういう武器を持って臨んでいる。それでも何人かは「引き込まれそうになった」と感じた。彼らの手口は相当洗練されている。僕の無防備な家族があの場にひとりでいたらどうなっていただろう。そう考えると、メ■ーマ■■をただネタ的・アトラクション的に消費しているだけではいけないのではないだろうか。この店長よりも強引な、もしくは■リー■■トよりも強引な手を使う者もいるはずだ。自分、そして家族の身を悪徳商法から守るため、僕たちはどうすれば良いのか。彼らの手口をもっとよく知っておく必要がありそうだ。

*1:さーちゃんが勝利した。

*2:https://www.youtube.com/watch?v=kbsr2qRxPMM

*3:放射線医学県民健康管理センターの調査結果（http://fukushima-mimamori.jp/outline/report/media/report_h26.pdf）によって否定されていることは調べればすぐにわかる。

*4:欠指症のことか？

2016-03-16

ブルーベリーの木

　とある村に、欠伸をする村人の開けた大口にブルーベリーをねじ込む男がいた。そのねじ込みがあまりに敏速であったため、誰も己の口内にブルーベリーが入るのを防ぐことができなかったという。最初の数年は、食糧不足もあったため、皆これを歓迎した。

　やがて農業が発達し、有無を言わさずブルーベリーをねじ込む彼は悪魔と呼ばれるようになった。村の人々から忌み嫌われる存在となったのだ。記録に残っている間、彼は一日も休むことなく、欠伸をする村人を探しては瞬く間に口の中へとブルーベリーをねじ込んだ。

　しかしある日、ブルーベリーねじ込みおじさんは村の権力者たちの卑怯な策略によって、五十数年の生涯に幕を閉じた。ブルーベリーねじ込みおじさんの死を悲しむ者は誰一人いなかった。遺体は極めて粗雑に扱われ、そのままの姿で埋められた。

　翌年、彼の消えた村には一本のブルーベリーの木が伸びていた。それの地面に根を張る様は村のどんな屈強な男も見惚れるほど力強く、まるでブルーベリーねじ込みおじさんの広大無辺の愛と勇気を称えているようであった。

2016-01-24

この文は偽である―命題に含まれる指差し語の問題―

（2016年4月2日　Y氏、L氏の指摘を受けて大幅に加筆修正）

　自己言及のパラドックスを引き起こす文の例として「この文は偽である」というものがよく挙げられる。「この文は偽である」が偽であると仮定すれば、「この文は真である」ことになり、仮定に反する。「この文は偽である」が真であると仮定すれば、「この文は偽である」ことになり、仮定に反する。したがってこの文はどうやっても矛盾を引き起こしてしまう、と言うのだ。よろしい。この（自己言及のパラドックスに関する）議論自体にまったく異論はない。しかしどうだろう、自己言及文の例として「この文は偽である」は適当だろうか。

　まず私の疑問、素朴な命題概念においては「この」の原理的な制限によって「この文は偽である」という文が「X: "X is false"」形式の自己言及文となり得ないのではないか、を検討してみよう。ゆえに本記事は「X: "X is false"」形式の自己言及文（つまりウソツキ文）が矛盾を引き起こすことの回避を目的としているわけではない。

　問題は「この」という語の使用法にある。通常、我々が「この」と言うときには、指差し、矢印、目線、文脈などを用いてなんらかの対象を指し示している。紙に書かれた文を指差しながら「この文は」と言う、紙に書かれた「この文は」からペンで矢印を別の文へとのばす、紙に書かれた文をちらりと見ながら「この文は」と言う、「『（文A）』、この文は」と続ける、等々。これらの動作をすべてあつめ、できた集合の元を単に「指差し動作」と呼ぶことにしよう*1。「この+指差し動作」ではじめて「この」はなんらかの対象を指し示すことができるのである。その通常の使用法に指差し動作が含まれるような語を以後「指差し語」と呼ぶ。

　さて、「この文は偽である」に含まれる指差し語「この」に、実際に対象を指差してもらおう。指差し動作は簡単に矢印で表す。

f:id:fukuso_sutaro:20160128203646p:plain

　「この文は偽である」という文が指差し動作の対象になっている。これでいいじゃないか、なんの問題もないだろう、と思ったそこのあなた。この図をよく見てほしい。指されている対象はあくまでも「『この文』は偽である」であって「『（この＋指差し動作）文』は偽である」ではない。指差し動作（ここでは矢印）がどうしてもはみ出てしまうのだ。つまり指差し動作の対象に含まれる「この文」は、指差し動作を含んだ指差し語ではなく、単なる「この文」という名詞なのだ。「この文」とはなんだろうか。まるで宙を眺めながら「これを見よ」と語りかけているようである。指差し動作を含まない「この文」はただ虚空を指しているのである。

　困った。これでは自己言及ができていないあまりか、言及対象が消えてしまっている。そこで、「この文」に「対応する指差し動作」と「この文は偽である」の両方を指差させてみよう。

f:id:fukuso_sutaro:20160128205410p:plain

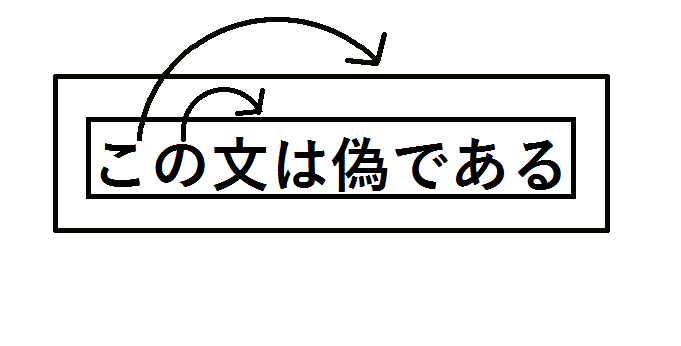
　これで「この文」の指差す対象は意味のある文になった。解決解決。なんだ、ちゃんと自己言及のパラドックスになっている。いや、果たしてそうだろうか。

　「この文」が指差す対象はなお「自己」ではない。実際、図では先ほどはみ出ていた矢印は指差し対象に取り込めたものの、新たな矢印がはみ出てしまっている。まあそんなことはどうでもいいのだ。矢印を増やしたことで、さらに深刻な問題が発生している。そもそも、指差し対象が常にひとつでなければならないことは直観的に明らかである。もしひとつの指差し語に指差し対象が複数対応していれば、我々はその対象ごとにそれぞれ真偽を考えなくてはならない。そのような文は命題として機能しない。よって、ふたつの矢印のうちどちらかは消去されねばならない。一方の矢印を消去すれば、結局は最初に提示した図とまったく同じ構造となってしまう。指差し語は自己言及文になることも、矛盾をつくりだすこともできないのだろうか。

①L氏との議論から見えてきた解決法

　TwitterのフォロワーであるL氏との議論から、私の言う「この」、つまり "This" の使用が論理学的使用と一致していないのではないかという仮説が出てきた。

　上記の指差し語的使用（日常的使用）を "Our-This" と呼び、論理学的使用を "S1-This" と呼ぶことにしよう*2。S1-This には "This sentence is false" を X: "X is false" に変換する作用があり、多くの論理学者は自然にその作用を受け入れ、"This" の使用のひとつに含まれるものと考えている。すると、私が神経質にこれらふたつの "This" を分けて（S1-This を除外して）いることに問題があり、指差し語は完全にスルーしてもよい議論だったということになる。

　しかし、現に私は自然に Our-This を採用していた。はじめから誰かが S1-This を提示してくれていれば、私や（存在するかわからないが）私と同じような疑問を持った者と論理学者たちの間の理解に齟齬が生じることもなかったのである。もし "This sentence is false" の多くの発話者が自然に This を論理学的に使用するのだとすれば、各々がふたつの使用の違いを自覚し、論理学的使用の合意が為されるべきではないか、と私は思う。

②Y氏との議論から見えてきた解決法

　ひとつ目の解決法は私の This の使いかたを修正するというものであったが、ふたつ目の解決法は私の（もしかすると他の多くの数学者の）命題概念を修正するというものである*3。

　"This sentence is false" のようなものも含め、発話可能な文を単に「文」と呼ぶ。文の中には見かけ上は命題と呼びうるもの（前－命題）が存在するが、それは命題ではない。命題は一般に文と文脈からつくられる、と考えてみよう。どれほど頑固な指差し語的使用主義者でも "This sentence is false" の言わんとしていることは十分に理解できる。なぜだろうか。それは我々が、文に付随する文脈を認識しているからである。指差し語が何を指差そうとしているかは「ウソツキ文の話をしている」「直近で他に真偽を問えるような文は出現していない」等々の文脈によって理解される。このように、文に必要なだけの文脈が与えられる*4と「指差し情報付き文」が生成される。指差し情報付き文の中に「真偽を問うことのできるもの」が存在するが、これを命題と呼ぶことにする。

　指差し語問題は前－命題と命題の混同、つまり指差し情報付き文が発話可能な（オブジェクトレベルの）指差し動作を含む文であると考えたことにより発生したが、実は本当に "This sentence is false" が言わんとしていることはメタレベルの発話によって伝達されていたのだ、ということである。つまり、指差し情報無しの文は命題ではなく、命題は発話できない。

　このように命題概念を修正すれば、指差し語問題はもはや命題に関する問題ではなくなり、無視してもよくなる。

　ここらへんの哲学的議論はまったく把握していないので、誰か似たようなことを問題にしていたら教えてほしい。

*1:後述の「指差し情報」とは別の概念である。

*2:L氏との議論でウソツキ文をS1と置いたため。

*3:L氏も似た指摘をしていた気がするのだが、私の中でうまく考えがまとめられていなかったので聞き逃してしまったかもしれない。

*4:文脈が必要になるのは、命題の真偽を問う段階ではなく、文から指差し情報付き文を生成する段階である。

2015-10-12

パソコンはまだ売っていますかね

　朝6時に絶叫しながら飛び起きた。マジかよ。寝たのは3時ごろじゃなかったか。確かに普段から絶叫しながら飛び起きているが、しかしこんなにも質の悪い目覚めは初めてだ。気持ち悪い。心臓がヤバい音を立てている。

　ということが今朝に――というかもう昨日の朝になってしまったが――あって、あまりにも衝撃的な（そして不愉快な）夢だったので忘れないうちに書き留めておくことにする。

　電車の中。あの、たいへん不快な息苦しさはたぶん、大阪市営地下鉄だろうと思う。僕は赤い座席に座っていて、左側には男が、右側には女が座っているのを視界の端で確認していた。男のほうは、大抵の成人男性がそうであるように、僕より体格が良いらしい。少し汚れたセンスのない服を着ている。女は中年だ。姿を見なくとも、なんとなく「あまり関わりたくないタイプのババア」であることがわかった。僕はあまり関わりたくないタイプのババアが嫌いだ。あまり関わりたくない。

　しばらく不審な挙動をしていると、隣の男が声をかけてきた。

「パソコンはまだ売っていますかね」

　――その異様な発音と抑揚に驚き、視線を左へちらりと移すと、そこにはこの世のものとは思えぬ異形の姿があった！　吐き気を催す極めて不安定なパーツの配置、醜く落ち窪んだ眼、そして強く憎悪を掻き立てるそのみすぼらしい表情！　ああ、なんということだ！　ここまでに悍ましい生き物が、忌むべき存在が、ここに在ることを許されているとでも言うのだろうか？　彼の冒涜的なフォルムを受け入れられる人間が世界にどれほどいるのだろうか。だがこの車両内でこの男に対しある種の感情を覚えている者は、驚くべきことに、ただのひとりもいないのである。僕は一瞬にして嘔吐寸前のところまでダメージを受けたが、いや、ここは公共交通機関だ、と懸命に耐え、男のほうを見ないようにした。

「パソコンはまだ売っていますかね」

　また男が話しかけてきた。パソコンなんてそこらの電気店で売っているだろう。こいつは何を聞いているんだ？　くらくらしながら横目で彼を見ると、その手には2丁の拳銃が握られていた。更に左隣の空席にも、拳銃が1丁あった。頭をゆらりゆらりと一定の周期で揺らしながら、異形の男は引き金をカチャカチャと触っていた。僕は咄嗟に大声を出し、男の手から拳銃を

　いや、こう文字に起こしてみると、なかなかこの気持ち悪さは伝わらないな。

2015-05-22

微分方程式メモ (4)

今回のテーマは積分定数だったが理解があまりにも不足しているので冪級数展開による解について書く。

$f(x,y)$ が複素変数 $x$ 、 $y$ についての複素数値函数である場合の微分方程式 $\frac{ dy}{dx}=f(x,y)$ について考えよう。 $f(x,y)$ は以下の条件に従うとする。
条件1':函数 $f(x,y)$ は $|x-x_0|＜a'$ 、 $|y-y_0|＜b'$ で与えられる複素平面の領域 $D'$ において $(x-x_0)$ と $(y-y_0)$ で収束冪級数に展開できる。つまり、 $f(x,y)$ は $D'$ で正則である。
この条件から、 $D'$ 内で $\frac{ ∂f(x,y)}{∂y }$ もまた正則であることがわかる。複素閉領域 $D$ を $|x-x_0|≦a$ 、 $|y-y_0|≦b$ $(0＜a＜a',0＜b＜b')$ で定めると、 $\frac{ ∂f(x,y)}{∂y }$ は $D$ で連続であるから、 $\left|\frac{ ∂f(x,y)}{∂y }\right|$ も $D$ で連続である。同様に $|f(x,y)|$ も $D$ で連続。有界閉集合上で連続なので、正数 $M$ と $K$ が存在して
$sup_{(x,y)∈D}|f(x,y)|=M＜\infty$
$sup_{(x,y)∈D}\left|\frac{ ∂f(x,y)}{∂y }\right|=K＜\infty$
を満たす。
$\frac{ ∂f(x,y)}{∂y }$ を $y_1$ と $y_2$ を繋ぐ線分に沿って積分することで以下の等式を得る。
$f(x,y_1)-f(x,y_2)=\int_{ y_1}^{ y_2}\frac{ ∂f(x,y)}{∂y }dy$
両辺に絶対値を付けて、
$|f(x,y_1)-f(x,y_2)|=\left|\int_{ y_1}^{ y_2}\frac{ ∂f(x,y)}{∂y }dy\right|$
$≦\int_{ y_1}^{ y_2}\left|\frac{ ∂f(x,y)}{∂y }\right| |dy|≦{\int_{ y_1}^{ y_2}K|dy|}=K|y_2-y_1|$
従って、 $f$ は $D$ 上でリプシッツ条件を満たす。
$|f(x,y_1)-f(x,y_2)|≦K|y_1-y_2|$
ゆえに、実数値函数の時と同じように、 $h=min\{a,\frac{ b}{M }\}$ とすると条件1'のもと $|x-x_0|≦h$ で微分方程式 $dy/dx=f(x,y)$ に逐次近似法を適用することが出来る。
$|x-x_0|≦h$ で $x_0$ と $x$ を繋ぐ滑らかな曲線に沿って複素積分する時、以下のように書ける。
$y_1(x)=y_0+\int_{ x_0}^{x }f(t,y(t))dt$
$y_2(x)=y_0+\int_{ x_0}^{x }f(t,y_1(t))dt$
…
$y_n(x)=y_0+\int_{ x_0}^{x }f(t,y_{n-1}(t))dt$
$f(x,y_0)$ は $|x-x_0|＜h$ で正則だから、最初の積分はwell-definedであり、曲線に依らず、それゆえ、 $y_1(x)$ もまたそうである。
最初の積分を取ると $y_1(x)-y_0=\int_{ x_0}^{x }f(t,y_0)dt$ だから、両辺に絶対値を付けて
$|y_1(x)-y_0|=\left|\int_{ x_0}^{x }f(t,y_0)dt\right|≦\int_{ x_0}^{x }|f(t,y_0)||dt|$
$≦\int_{x_0}^{x}M|dt|≦M|x-x_0|＜hM≦\frac{ b}{ M}M=b$
よって $f(x,y_1(x))$ は $|x-x_0|＜h≦a$ で $x$ の函数としてwell-definedである。
$y_1(x)$ が正則函数 $f(x,y_0)$ の積分により与えられることから、 $y_1(x)$ は $|x-x_0|＜h$ で正則である。従って、2つ目の積分 $\int_{x_0}^{x}f(t,y_1(t))dt$ はwell-definedであり、 $y_2(x)$ も $|x-x_0|＜h$ においてwell-definedかつ正則である。 $x_0$ と $x$ を繋ぐ線分に沿って積分すると、
$|y_2(x)-y_0|≦ \left| \int_{x_0}^{x} f(t,y_1(t))dt \right|≦ \int_{x_0}^{x}|f(t,y_1(t))||dt|$
$≦\int_{x_0}^{x}M|dt|≦M|x-x_0|＜hM≦b$
このようにして $|x-x_0|＜h$ で $y_3(x)$ 、 $y_4(x)$ 、 $y_5(x)$ 、… を次々と定義することができる。
実際、上の事実から簡単にわかるように $y_k(x)$ が $|x-x_0|＜h$ でwell-definedかつ正則と仮定すると $|y_{k+1}(x)-y_0|＜b$ となり $y_{k+1}(x)$ も $|x-x_0|＜h$ でwell-definedである。よって、函数 $y_n(x)$ $(n∈\mathbb{N}\setminus \{0\})$ は $|x-x_0|＜h$ で正則かつ $|y_n(x)-y_0|＜b$ 。
$x_0$ と $x$ を繋ぐ線分に沿った積分を取ることと、微分方程式メモ (1)と同様の計算により、正則函数列 ${(y_n(x))}_{n∈\mathbb{N}}$ の $|x-x_0|＜h$ での一様収束性と、 $y(x_0)=y_0$ 、 $\frac{dy}{dx}=f(x,y)$ を満たす極限函数 $y(x)$ が示せる。更に、正則函数列の一様極限 $y(x)$ もまた正則である。
解の一意性は実数値函数の時と同様に証明される。

2015-05-17

微分方程式メモ (3)

今回は $n$ 次近似解の誤差評価について。
微分方程式メモ(1)で得た不等式
$|y_m(x)-y_n(x)|≦b\sum_{k=n}^{m-1}\frac{{(Kh)}^k}{k!}$
で $m \to \infty$ として、区間 $|x-x_0|≦h$ で
$|y(x)-y_n(x)|≦b\sum_{k=n}^{\infty}\frac{{(Kh)}^k}{k!}$
を得る。この不等式は $n$ 次近似解 $y_n(x)$ の誤差評価となっている。しかしこの評価法では何度も積分の評価を繰り返す必要があり、いつも実用的な方法であるとは限らない。
別のやり方を考えてみよう。 $f(x,y)$ の近似 $g(x,y)$ を初期条件 $z(x_0)=y_0$ を満たす区間 $|x-x_0|≦h$ 上で微分方程式 $\frac{dz}{dx}=g(x,y)$ の解 $z(x)$ を見つけることができるようなものであるとする。正数 $ε$ は $sup_{(x,y)∈D}|f(x,y)-g(x,y)|≦ε$ を満たすとする。そして $y(x)$ を初期条件 $y(x_0)=y_0$ を満たす $|x-x_0|≦h$ における $\frac{dy}{dx}=g(x,y)$ のuniqueな解とする。この時、
$|y(x)-z(x)|=\left|\int_{x_0}^{x}f(t,y(t))dt-\int_{x_0}^{x}g(t,z(t))dt\right|=\left|\int_{x_0}^{x}f(t,y(t))-g(t,z(t))dt\right|$
リプシッツ条件より以下の不等式が導かれる。
$|y(x)-z(x)|=\left|\int_{x_0}^{x}f(t,y(t))-g(t,z(t))dt\right|$
$=\left|\int_{x_0}^{x}f(t,y(t))-f(t,z(t))+f(t,z(t))-g(t,z(t))dt\right|$
$=\left|\int_{x_0}^{x}f(t,y(t))-f(t,z(t))dt+\int_{x_0}^{x}f(t,z(t))-g(t,z(t))dt\right|$
$=\left|\int_{x_0}^{x}f(t,y(t))-f(t,z(t))dt+\int_{x_0}^{x}f(t,z(t))-g(t,z(t))dt\right|$
$≦\left|\int_{x_0}^{x}f(t,y(t))-f(t,z(t))dt\right|+\left|\int_{x_0}^{x}f(t,z(t))-g(t,z(t))dt\right|$
$≦\left|\int_{x_0}^{x}|f(t,y(t))-f(t,z(t))|dt\right|+\left|\int_{x_0}^{x}|f(t,z(t))-g(t,z(t))|dt\right|$
$≦|ε|x-x_0||+\left|\int_{x_0}^{x}K|y(t)-z(t)|dt\right|$
$=ε|x-x_0|+K\left|\int_{x_0}^{x}|y(t)-z(t)|dt\right|$
ゆえに、 $L=sup_{|x-x_0|≦h}|y(x)-z(x)|$ とおくと、
$|y(x)-z(x)|≦ε|x-x_0|+K\left|\int_{x_0}^{x}|y(t)-z(t)|dt\right|$
$≦ε|x-x_0|+KL|x-x_0|$
上の不等式 $|y(x)-z(x)|≦ε|x-x_0|+K\left|\int_{x_0}^{x}|y(t)-z(t)|dt\right|$ の右辺の $|y(t)-z(t)|$ をこの不等式で評価すると、
$|y(x)-z(x)|≦ε|x-x_0|+K\left|\int_{x_0}^{x}|y(t)-z(t)|dt\right|$
$≦ε|x-x_0|+K\left|\int_{x_0}^{x}ε|t-x_0|+KL|t-x_0|dt\right|$
$≦ε|x-x_0|+K\left|\frac{ε{|x-x_0|}^2}{2}+\frac{KL{|x-x_0|}^2}{2}\right|$
$≦ε|x-x_0|+\frac{Kε{|x-x_0|}^2}{2}+\frac{K^2L{|x-x_0|}^2}{2}$
ここから紆余曲折あって $|x-x_0|≦h$ 上で任意の $n∈\mathbb{N}\setminus\{0\}$ に対し
$|y(x)-z(x)|≦\frac{L{(K|x-x_0|)}^n}{n!}+ε\sum_{m=1}^{n}\frac{K^{m-1}{|x-x_0|}^m}{m!}$
であることが言える。
この不等式の右辺を $n\to\infty$ とすれば、第1項は $0$ に一様収束し、第2項は $ε\frac{e^{K|x-x_0|}-1}{K}$ より小さくなる。
実際、
$ε\sum_{m=1}^{n}\frac{K^{m-1}{|x-x_0|}^m}{m!}=\frac{ε}{K}\sum_{m=1}^{n}\frac{{(K|x-x_0|)}^m}{m!}$
$=\frac{ε}{K}\left(\sum_{m=0}^{n}\frac{{(K|x-x_0|)}^m}{m!}-1\right)$
$=\frac{ε}{K}\left(\sum_{m=0}^{\infty}\frac{{(K|x-x_0|)}^m}{m!}-1-\sum_{l=n+1}^{\infty}\frac{{(K|x-x_0|)}^l}{l!}\right)$
$=\frac{ε}{K}\left(e^{K|x-x_0|}-1-\sum_{l=n+1}^{\infty}\frac{{(K|x-x_0|)}^l}{l!}\right)$
$≦ε\frac{e^{K|x-x_0|}-1}{K}$
よって、 $|x-x_0|≦h$ での近似解 $z(x)$ の誤差評価は以下の不等式で与えられる。
$|y(x)-z(x)|≦ε\frac{e^{K|x-x_0|}-1}{K}$

次回は積分定数について書く予定だが数式を打ち込むのに疲れてきたので飛ばすかもしれない。

2015-05-09

微分方程式メモ (2)

予告した通り今回は解の一意性について書く。まだ1日も経っていないがしばらく数式を打ち込んでいられる余裕も無さそうだから早めに投稿した。あくまでもメモであって、人に見せることは考えずに書いているので注意。

逐次近似法により $y(x_0)=y_0$ を満足する $dy/dx=f(x,y)$ の解 $y(x)$ を得た。しかし、 $dy/dx=f(x,y)$ の解の一意性についてまだ確かめていない。同じ初期条件を満たす別の解がある可能性が残っているのだ。
前回のメモで設定した以下の2つの条件の下、一意性を証明する。
条件1:函数 $f(x,y)$ は実数値で、 $|x-x_0|≦a$ 、 $|y-y_0|≦b$ $(a,b＞0)$ で定義される $(x,y)$ 平面の領域 $D$ で連続である。
条件2: $f(x,y)$ は $D$ で $y$ に関してリプシッツ条件を満たす。つまり、正定数 $K$ が存在し $D$ の任意の点の組 $(x_1,y_1)$ 、 $(x_2,y_2)$ に対し
$|f(x_1,y_1)-f(x_2,y_2)|≦K|y_1-y_2|$
が成り立つ。
[証明]
$z(x)$ を $z(x_0)=y_0$ 、 $z(x)=y_0+\int_{x_0}^{x}f(t,z(t))dt$ を満たす $dy/dx=f(x,y)$ の解とする。
条件2より、
$|y(x)-z(x)|=\left|y_0+\int_{x_0}^{x}f(t,y(t))dt-y_0-\int_{x_0}^{x}f(t,z(x))dt\right|$
$=\left|\int_{x_0}^{x}f(t,y(t))dt-\int_{x_0}^{x}f(t,z(x))dt\right|$ $=\left|\int_{x_0}^{x}f(t,y(t))dt-f(t,z(x))dt\right|$
$≦\left|\int_{x_0}^{x}K|y(t)-z(t)|dt\right|=K\left|\int_{x_0}^{x}|y(t)-z(t)|dt\right|$
ここで $N=sup_{|x-x_0|≦h}|y(x)-z(x)|$ とおくと、 $|x-x_0|≦h$ で
$|y(x)-z(x)|≦KN|x-x_0|$
この不等式で $|y(x)-z(x)|≦K\left|\int_{x_0}^{x}|y(t)-z(t)|dt\right|$ の右辺の $|y(t)-z(t)|$ を評価すると、
$|y(x)-z(x)|≦K\left|\int_{x_0}^{x}|y(t)-z(t)|dt\right|≦K\left|\int_{x_0}^{x}KN|t-x_0| dt\right|$
$=K^{2}N\left|\int_{x_0}^{x}|t-x_0|dt\right|=K^{2}N\frac{{|x-x_0|}^{2}}{2}≦\frac{N(Kh)^{2}}{2}$
さて、 $|y(x)-z(x)|≦\frac{N(K|x-x_0|)^{n-1}}{(n-1)!}$ であるとすれば
$|y(x)-z(x)|≦K\left|\int_{x_0}^{x}|y(t)-z(t)|dt\right|≦K\left|\int_{x_0}^{x}\frac{N(K|t-x_0|)^{n-1}}{(n-1)!}dt\right|$
$=K^{n}N\left|\int_{x_0}^{x}\frac{{|t-x_0|}^{n-1}}{(n-1)!}dt\right|≦K^{n}N\frac{{|x-x_0|}^{n}}{n!}$
$=\frac{N{(K|x-x_0|)}^{n}}{n!}≦\frac{N{(Kh)}^{n}}{n!}$
よって任意の $m$ に対し $|y(x)-z(x)|≦\frac{N{(Kh)}^{m}}{m!}$ が成立。
右辺は $x$ の選び方に依らないので $N≦\frac{N{(Kh)}^{m}}{m!}$ が言える。しかし $\frac{{(Kh)}^{m}}{m!}$ は $m$ を大きくしていくと $1$ より真に小さくなり、 $N=0$ でなければこの不等式は成り立たない。
$|y(x)-z(x)|≦N=0$ より $y(x)=z(x)$ であるから、解は一意的である。証明終。

逐次近似法の手順を説明するため、ひとつ例を見てみよう。
初期条件 $y(0)=1$ の下で、 $\frac{dy}{dx}=y(x)$ を解く。前回のメモと同じようにして函数列 ${(y_n(x))}_{n∈ \bf N}$ を定義する:
$y_0(x)=y_0=1$
$y_1(x)=y_0+\int_{x_0}^{x}f(t,y_0)dt=1+\int_{0}^{x}1dt=1+x$
$y_2(x)=y_0+\int_{x_0}^{x}f(t,y_1(t))dt=1+\int_{0}^{x}1+tdt=1+x+\frac{x^2}{2}$
$y_3(x)=y_0+\int_{x_0}^{x}f(t,y_2(t))dt=1+\int_{0}^{x}1+t+\frac{t^2}{2}dt=1+x+\frac{x^2}{2}+\frac{x^3}{6}$
…
以上から $y_n(x)=\sum_{k=0}^{n}\frac{x^k}{k!}$ と予想できる。 $n=1$ の時は成立している。
$y_{n-1}(x)=\sum_{k=0}^{n-1}\frac{x^k}{k!}$ と仮定すると、
$y_n(x)=1+\int_{0}^{x}\sum_{k=0}^{n-1}\frac{t^k}{k!}dt=1+\sum_{k=0}^{n-1}\int_{0}^{x}\frac{t^k}{k!}dt$
$=1+\sum_{k=1}^{n}\int_{0}^{x}\frac{t^{k-1}}{(k-1)!}dt=1+\sum_{k=1}^{n}\frac{x^k}{k!}=\sum_{k=0}^{n}\frac{x^k}{k!}$
従って、先程の予想は正しい。
微分方程式 $dy/dx=y(x)$ の解 $\lim_{n \to \infty}y_n(x)=y(x)$ は、
$\lim_{n \to \infty}y_n(x)=\lim_{n \to \infty}\sum_{k=0}^{n}\frac{x^k}{k!}=\sum_{k=0}^{\infty}\frac{x^k}{k!}$
こうして $y(x)=exp(x):=e^x$ が導かれた。

次回は $n$ 次近似解 $y_n(x)$ の誤差評価について書く予定。