2016-03-16

ブルーベリーの木

　とある村に、欠伸をする村人の開けた大口にブルーベリーをねじ込む男がいた。そのねじ込みがあまりに敏速であったため、誰も己の口内にブルーベリーが入るのを防ぐことができなかったという。最初の数年は、食糧不足もあったため、皆これを歓迎した。

　やがて農業が発達し、有無を言わさずブルーベリーをねじ込む彼は悪魔と呼ばれるようになった。村の人々から忌み嫌われる存在となったのだ。記録に残っている間、彼は一日も休むことなく、欠伸をする村人を探しては瞬く間に口の中へとブルーベリーをねじ込んだ。

　しかしある日、ブルーベリーねじ込みおじさんは村の権力者たちの卑怯な策略によって、五十数年の生涯に幕を閉じた。ブルーベリーねじ込みおじさんの死を悲しむ者は誰一人いなかった。遺体は極めて粗雑に扱われ、そのままの姿で埋められた。

　翌年、彼の消えた村には一本のブルーベリーの木が伸びていた。それの地面に根を張る様は村のどんな屈強な男も見惚れるほど力強く、まるでブルーベリーねじ込みおじさんの広大無辺の愛と勇気を称えているようであった。

2016-01-24

この文は偽である―命題に含まれる指差し語の問題―

（2016年4月2日　Y氏、L氏の指摘を受けて大幅に加筆修正）

　自己言及のパラドックスを引き起こす文の例として「この文は偽である」というものがよく挙げられる。「この文は偽である」が偽であると仮定すれば、「この文は真である」ことになり、仮定に反する。「この文は偽である」が真であると仮定すれば、「この文は偽である」ことになり、仮定に反する。したがってこの文はどうやっても矛盾を引き起こしてしまう、と言うのだ。よろしい。この（自己言及のパラドックスに関する）議論自体にまったく異論はない。しかしどうだろう、自己言及文の例として「この文は偽である」は適当だろうか。

　まず私の疑問、素朴な命題概念においては「この」の原理的な制限によって「この文は偽である」という文が「X: "X is false"」形式の自己言及文となり得ないのではないか、を検討してみよう。ゆえに本記事は「X: "X is false"」形式の自己言及文（つまりウソツキ文）が矛盾を引き起こすことの回避を目的としているわけではない。

　問題は「この」という語の使用法にある。通常、我々が「この」と言うときには、指差し、矢印、目線、文脈などを用いてなんらかの対象を指し示している。紙に書かれた文を指差しながら「この文は」と言う、紙に書かれた「この文は」からペンで矢印を別の文へとのばす、紙に書かれた文をちらりと見ながら「この文は」と言う、「『（文A）』、この文は」と続ける、等々。これらの動作をすべてあつめ、できた集合の元を単に「指差し動作」と呼ぶことにしよう*1。「この+指差し動作」ではじめて「この」はなんらかの対象を指し示すことができるのである。その通常の使用法に指差し動作が含まれるような語を以後「指差し語」と呼ぶ。

　さて、「この文は偽である」に含まれる指差し語「この」に、実際に対象を指差してもらおう。指差し動作は簡単に矢印で表す。

f:id:fukuso_sutaro:20160128203646p:plain

　「この文は偽である」という文が指差し動作の対象になっている。これでいいじゃないか、なんの問題もないだろう、と思ったそこのあなた。この図をよく見てほしい。指されている対象はあくまでも「『この文』は偽である」であって「『（この＋指差し動作）文』は偽である」ではない。指差し動作（ここでは矢印）がどうしてもはみ出てしまうのだ。つまり指差し動作の対象に含まれる「この文」は、指差し動作を含んだ指差し語ではなく、単なる「この文」という名詞なのだ。「この文」とはなんだろうか。まるで宙を眺めながら「これを見よ」と語りかけているようである。指差し動作を含まない「この文」はただ虚空を指しているのである。

　困った。これでは自己言及ができていないあまりか、言及対象が消えてしまっている。そこで、「この文」に「対応する指差し動作」と「この文は偽である」の両方を指差させてみよう。

f:id:fukuso_sutaro:20160128205410p:plain

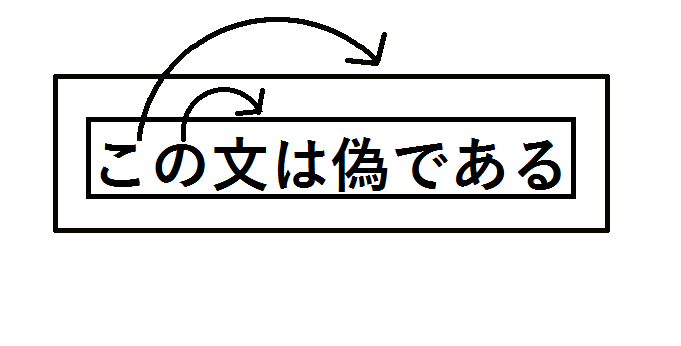
　これで「この文」の指差す対象は意味のある文になった。解決解決。なんだ、ちゃんと自己言及のパラドックスになっている。いや、果たしてそうだろうか。

　「この文」が指差す対象はなお「自己」ではない。実際、図では先ほどはみ出ていた矢印は指差し対象に取り込めたものの、新たな矢印がはみ出てしまっている。まあそんなことはどうでもいいのだ。矢印を増やしたことで、さらに深刻な問題が発生している。そもそも、指差し対象が常にひとつでなければならないことは直観的に明らかである。もしひとつの指差し語に指差し対象が複数対応していれば、我々はその対象ごとにそれぞれ真偽を考えなくてはならない。そのような文は命題として機能しない。よって、ふたつの矢印のうちどちらかは消去されねばならない。一方の矢印を消去すれば、結局は最初に提示した図とまったく同じ構造となってしまう。指差し語は自己言及文になることも、矛盾をつくりだすこともできないのだろうか。

①L氏との議論から見えてきた解決法

　TwitterのフォロワーであるL氏との議論から、私の言う「この」、つまり "This" の使用が論理学的使用と一致していないのではないかという仮説が出てきた。

　上記の指差し語的使用（日常的使用）を "Our-This" と呼び、論理学的使用を "S1-This" と呼ぶことにしよう*2。S1-This には "This sentence is false" を X: "X is false" に変換する作用があり、多くの論理学者は自然にその作用を受け入れ、"This" の使用のひとつに含まれるものと考えている。すると、私が神経質にこれらふたつの "This" を分けて（S1-This を除外して）いることに問題があり、指差し語は完全にスルーしてもよい議論だったということになる。

　しかし、現に私は自然に Our-This を採用していた。はじめから誰かが S1-This を提示してくれていれば、私や（存在するかわからないが）私と同じような疑問を持った者と論理学者たちの間の理解に齟齬が生じることもなかったのである。もし "This sentence is false" の多くの発話者が自然に This を論理学的に使用するのだとすれば、各々がふたつの使用の違いを自覚し、論理学的使用の合意が為されるべきではないか、と私は思う。

②Y氏との議論から見えてきた解決法

　ひとつ目の解決法は私の This の使いかたを修正するというものであったが、ふたつ目の解決法は私の（もしかすると他の多くの数学者の）命題概念を修正するというものである*3。

　"This sentence is false" のようなものも含め、発話可能な文を単に「文」と呼ぶ。文の中には見かけ上は命題と呼びうるもの（前－命題）が存在するが、それは命題ではない。命題は一般に文と文脈からつくられる、と考えてみよう。どれほど頑固な指差し語的使用主義者でも "This sentence is false" の言わんとしていることは十分に理解できる。なぜだろうか。それは我々が、文に付随する文脈を認識しているからである。指差し語が何を指差そうとしているかは「ウソツキ文の話をしている」「直近で他に真偽を問えるような文は出現していない」等々の文脈によって理解される。このように、文に必要なだけの文脈が与えられる*4と「指差し情報付き文」が生成される。指差し情報付き文の中に「真偽を問うことのできるもの」が存在するが、これを命題と呼ぶことにする。

　指差し語問題は前－命題と命題の混同、つまり指差し情報付き文が発話可能な（オブジェクトレベルの）指差し動作を含む文であると考えたことにより発生したが、実は本当に "This sentence is false" が言わんとしていることはメタレベルの発話によって伝達されていたのだ、ということである。つまり、指差し情報無しの文は命題ではなく、命題は発話できない。

　このように命題概念を修正すれば、指差し語問題はもはや命題に関する問題ではなくなり、無視してもよくなる。

　ここらへんの哲学的議論はまったく把握していないので、誰か似たようなことを問題にしていたら教えてほしい。

*1:後述の「指差し情報」とは別の概念である。

*2:L氏との議論でウソツキ文をS1と置いたため。

*3:L氏も似た指摘をしていた気がするのだが、私の中でうまく考えがまとめられていなかったので聞き逃してしまったかもしれない。

*4:文脈が必要になるのは、命題の真偽を問う段階ではなく、文から指差し情報付き文を生成する段階である。

2015-10-12

パソコンはまだ売っていますかね

　朝6時に絶叫しながら飛び起きた。マジかよ。寝たのは3時ごろじゃなかったか。確かに普段から絶叫しながら飛び起きているが、しかしこんなにも質の悪い目覚めは初めてだ。気持ち悪い。心臓がヤバい音を立てている。

　ということが今朝に――というかもう昨日の朝になってしまったが――あって、あまりにも衝撃的な（そして不愉快な）夢だったので忘れないうちに書き留めておくことにする。

　電車の中。あの、たいへん不快な息苦しさはたぶん、大阪市営地下鉄だろうと思う。僕は赤い座席に座っていて、左側には男が、右側には女が座っているのを視界の端で確認していた。男のほうは、大抵の成人男性がそうであるように、僕より体格が良いらしい。少し汚れたセンスのない服を着ている。女は中年だ。姿を見なくとも、なんとなく「あまり関わりたくないタイプのババア」であることがわかった。僕はあまり関わりたくないタイプのババアが嫌いだ。あまり関わりたくない。

　しばらく不審な挙動をしていると、隣の男が声をかけてきた。

「パソコンはまだ売っていますかね」

　――その異様な発音と抑揚に驚き、視線を左へちらりと移すと、そこにはこの世のものとは思えぬ異形の姿があった！　吐き気を催す極めて不安定なパーツの配置、醜く落ち窪んだ眼、そして強く憎悪を掻き立てるそのみすぼらしい表情！　ああ、なんということだ！　ここまでに悍ましい生き物が、忌むべき存在が、ここに在ることを許されているとでも言うのだろうか？　彼の冒涜的なフォルムを受け入れられる人間が世界にどれほどいるのだろうか。だがこの車両内でこの男に対しある種の感情を覚えている者は、驚くべきことに、ただのひとりもいないのである。僕は一瞬にして嘔吐寸前のところまでダメージを受けたが、いや、ここは公共交通機関だ、と懸命に耐え、男のほうを見ないようにした。

「パソコンはまだ売っていますかね」

　また男が話しかけてきた。パソコンなんてそこらの電気店で売っているだろう。こいつは何を聞いているんだ？　くらくらしながら横目で彼を見ると、その手には2丁の拳銃が握られていた。更に左隣の空席にも、拳銃が1丁あった。頭をゆらりゆらりと一定の周期で揺らしながら、異形の男は引き金をカチャカチャと触っていた。僕は咄嗟に大声を出し、男の手から拳銃を

　いや、こう文字に起こしてみると、なかなかこの気持ち悪さは伝わらないな。

2015-05-22

微分方程式メモ (4)

今回のテーマは積分定数だったが理解があまりにも不足しているので冪級数展開による解について書く。

$f(x,y)$ が複素変数 $x$ 、 $y$ についての複素数値函数である場合の微分方程式 $\frac{ dy}{dx}=f(x,y)$ について考えよう。 $f(x,y)$ は以下の条件に従うとする。
条件1':函数 $f(x,y)$ は $|x-x_0|＜a'$ 、 $|y-y_0|＜b'$ で与えられる複素平面の領域 $D'$ において $(x-x_0)$ と $(y-y_0)$ で収束冪級数に展開できる。つまり、 $f(x,y)$ は $D'$ で正則である。
この条件から、 $D'$ 内で $\frac{ ∂f(x,y)}{∂y }$ もまた正則であることがわかる。複素閉領域 $D$ を $|x-x_0|≦a$ 、 $|y-y_0|≦b$ $(0＜a＜a',0＜b＜b')$ で定めると、 $\frac{ ∂f(x,y)}{∂y }$ は $D$ で連続であるから、 $\left|\frac{ ∂f(x,y)}{∂y }\right|$ も $D$ で連続である。同様に $|f(x,y)|$ も $D$ で連続。有界閉集合上で連続なので、正数 $M$ と $K$ が存在して
$sup_{(x,y)∈D}|f(x,y)|=M＜\infty$
$sup_{(x,y)∈D}\left|\frac{ ∂f(x,y)}{∂y }\right|=K＜\infty$
を満たす。
$\frac{ ∂f(x,y)}{∂y }$ を $y_1$ と $y_2$ を繋ぐ線分に沿って積分することで以下の等式を得る。
$f(x,y_1)-f(x,y_2)=\int_{ y_1}^{ y_2}\frac{ ∂f(x,y)}{∂y }dy$
両辺に絶対値を付けて、
$|f(x,y_1)-f(x,y_2)|=\left|\int_{ y_1}^{ y_2}\frac{ ∂f(x,y)}{∂y }dy\right|$
$≦\int_{ y_1}^{ y_2}\left|\frac{ ∂f(x,y)}{∂y }\right| |dy|≦{\int_{ y_1}^{ y_2}K|dy|}=K|y_2-y_1|$
従って、 $f$ は $D$ 上でリプシッツ条件を満たす。
$|f(x,y_1)-f(x,y_2)|≦K|y_1-y_2|$
ゆえに、実数値函数の時と同じように、 $h=min\{a,\frac{ b}{M }\}$ とすると条件1'のもと $|x-x_0|≦h$ で微分方程式 $dy/dx=f(x,y)$ に逐次近似法を適用することが出来る。
$|x-x_0|≦h$ で $x_0$ と $x$ を繋ぐ滑らかな曲線に沿って複素積分する時、以下のように書ける。
$y_1(x)=y_0+\int_{ x_0}^{x }f(t,y(t))dt$
$y_2(x)=y_0+\int_{ x_0}^{x }f(t,y_1(t))dt$
…
$y_n(x)=y_0+\int_{ x_0}^{x }f(t,y_{n-1}(t))dt$
$f(x,y_0)$ は $|x-x_0|＜h$ で正則だから、最初の積分はwell-definedであり、曲線に依らず、それゆえ、 $y_1(x)$ もまたそうである。
最初の積分を取ると $y_1(x)-y_0=\int_{ x_0}^{x }f(t,y_0)dt$ だから、両辺に絶対値を付けて
$|y_1(x)-y_0|=\left|\int_{ x_0}^{x }f(t,y_0)dt\right|≦\int_{ x_0}^{x }|f(t,y_0)||dt|$
$≦\int_{x_0}^{x}M|dt|≦M|x-x_0|＜hM≦\frac{ b}{ M}M=b$
よって $f(x,y_1(x))$ は $|x-x_0|＜h≦a$ で $x$ の函数としてwell-definedである。
$y_1(x)$ が正則函数 $f(x,y_0)$ の積分により与えられることから、 $y_1(x)$ は $|x-x_0|＜h$ で正則である。従って、2つ目の積分 $\int_{x_0}^{x}f(t,y_1(t))dt$ はwell-definedであり、 $y_2(x)$ も $|x-x_0|＜h$ においてwell-definedかつ正則である。 $x_0$ と $x$ を繋ぐ線分に沿って積分すると、
$|y_2(x)-y_0|≦ \left| \int_{x_0}^{x} f(t,y_1(t))dt \right|≦ \int_{x_0}^{x}|f(t,y_1(t))||dt|$
$≦\int_{x_0}^{x}M|dt|≦M|x-x_0|＜hM≦b$
このようにして $|x-x_0|＜h$ で $y_3(x)$ 、 $y_4(x)$ 、 $y_5(x)$ 、… を次々と定義することができる。
実際、上の事実から簡単にわかるように $y_k(x)$ が $|x-x_0|＜h$ でwell-definedかつ正則と仮定すると $|y_{k+1}(x)-y_0|＜b$ となり $y_{k+1}(x)$ も $|x-x_0|＜h$ でwell-definedである。よって、函数 $y_n(x)$ $(n∈\mathbb{N}\setminus \{0\})$ は $|x-x_0|＜h$ で正則かつ $|y_n(x)-y_0|＜b$ 。
$x_0$ と $x$ を繋ぐ線分に沿った積分を取ることと、微分方程式メモ (1)と同様の計算により、正則函数列 ${(y_n(x))}_{n∈\mathbb{N}}$ の $|x-x_0|＜h$ での一様収束性と、 $y(x_0)=y_0$ 、 $\frac{dy}{dx}=f(x,y)$ を満たす極限函数 $y(x)$ が示せる。更に、正則函数列の一様極限 $y(x)$ もまた正則である。
解の一意性は実数値函数の時と同様に証明される。

2015-05-17

微分方程式メモ (3)

今回は $n$ 次近似解の誤差評価について。
微分方程式メモ(1)で得た不等式
$|y_m(x)-y_n(x)|≦b\sum_{k=n}^{m-1}\frac{{(Kh)}^k}{k!}$
で $m \to \infty$ として、区間 $|x-x_0|≦h$ で
$|y(x)-y_n(x)|≦b\sum_{k=n}^{\infty}\frac{{(Kh)}^k}{k!}$
を得る。この不等式は $n$ 次近似解 $y_n(x)$ の誤差評価となっている。しかしこの評価法では何度も積分の評価を繰り返す必要があり、いつも実用的な方法であるとは限らない。
別のやり方を考えてみよう。 $f(x,y)$ の近似 $g(x,y)$ を初期条件 $z(x_0)=y_0$ を満たす区間 $|x-x_0|≦h$ 上で微分方程式 $\frac{dz}{dx}=g(x,y)$ の解 $z(x)$ を見つけることができるようなものであるとする。正数 $ε$ は $sup_{(x,y)∈D}|f(x,y)-g(x,y)|≦ε$ を満たすとする。そして $y(x)$ を初期条件 $y(x_0)=y_0$ を満たす $|x-x_0|≦h$ における $\frac{dy}{dx}=g(x,y)$ のuniqueな解とする。この時、
$|y(x)-z(x)|=\left|\int_{x_0}^{x}f(t,y(t))dt-\int_{x_0}^{x}g(t,z(t))dt\right|=\left|\int_{x_0}^{x}f(t,y(t))-g(t,z(t))dt\right|$
リプシッツ条件より以下の不等式が導かれる。
$|y(x)-z(x)|=\left|\int_{x_0}^{x}f(t,y(t))-g(t,z(t))dt\right|$
$=\left|\int_{x_0}^{x}f(t,y(t))-f(t,z(t))+f(t,z(t))-g(t,z(t))dt\right|$
$=\left|\int_{x_0}^{x}f(t,y(t))-f(t,z(t))dt+\int_{x_0}^{x}f(t,z(t))-g(t,z(t))dt\right|$
$=\left|\int_{x_0}^{x}f(t,y(t))-f(t,z(t))dt+\int_{x_0}^{x}f(t,z(t))-g(t,z(t))dt\right|$
$≦\left|\int_{x_0}^{x}f(t,y(t))-f(t,z(t))dt\right|+\left|\int_{x_0}^{x}f(t,z(t))-g(t,z(t))dt\right|$
$≦\left|\int_{x_0}^{x}|f(t,y(t))-f(t,z(t))|dt\right|+\left|\int_{x_0}^{x}|f(t,z(t))-g(t,z(t))|dt\right|$
$≦|ε|x-x_0||+\left|\int_{x_0}^{x}K|y(t)-z(t)|dt\right|$
$=ε|x-x_0|+K\left|\int_{x_0}^{x}|y(t)-z(t)|dt\right|$
ゆえに、 $L=sup_{|x-x_0|≦h}|y(x)-z(x)|$ とおくと、
$|y(x)-z(x)|≦ε|x-x_0|+K\left|\int_{x_0}^{x}|y(t)-z(t)|dt\right|$
$≦ε|x-x_0|+KL|x-x_0|$
上の不等式 $|y(x)-z(x)|≦ε|x-x_0|+K\left|\int_{x_0}^{x}|y(t)-z(t)|dt\right|$ の右辺の $|y(t)-z(t)|$ をこの不等式で評価すると、
$|y(x)-z(x)|≦ε|x-x_0|+K\left|\int_{x_0}^{x}|y(t)-z(t)|dt\right|$
$≦ε|x-x_0|+K\left|\int_{x_0}^{x}ε|t-x_0|+KL|t-x_0|dt\right|$
$≦ε|x-x_0|+K\left|\frac{ε{|x-x_0|}^2}{2}+\frac{KL{|x-x_0|}^2}{2}\right|$
$≦ε|x-x_0|+\frac{Kε{|x-x_0|}^2}{2}+\frac{K^2L{|x-x_0|}^2}{2}$
ここから紆余曲折あって $|x-x_0|≦h$ 上で任意の $n∈\mathbb{N}\setminus\{0\}$ に対し
$|y(x)-z(x)|≦\frac{L{(K|x-x_0|)}^n}{n!}+ε\sum_{m=1}^{n}\frac{K^{m-1}{|x-x_0|}^m}{m!}$
であることが言える。
この不等式の右辺を $n\to\infty$ とすれば、第1項は $0$ に一様収束し、第2項は $ε\frac{e^{K|x-x_0|}-1}{K}$ より小さくなる。
実際、
$ε\sum_{m=1}^{n}\frac{K^{m-1}{|x-x_0|}^m}{m!}=\frac{ε}{K}\sum_{m=1}^{n}\frac{{(K|x-x_0|)}^m}{m!}$
$=\frac{ε}{K}\left(\sum_{m=0}^{n}\frac{{(K|x-x_0|)}^m}{m!}-1\right)$
$=\frac{ε}{K}\left(\sum_{m=0}^{\infty}\frac{{(K|x-x_0|)}^m}{m!}-1-\sum_{l=n+1}^{\infty}\frac{{(K|x-x_0|)}^l}{l!}\right)$
$=\frac{ε}{K}\left(e^{K|x-x_0|}-1-\sum_{l=n+1}^{\infty}\frac{{(K|x-x_0|)}^l}{l!}\right)$
$≦ε\frac{e^{K|x-x_0|}-1}{K}$
よって、 $|x-x_0|≦h$ での近似解 $z(x)$ の誤差評価は以下の不等式で与えられる。
$|y(x)-z(x)|≦ε\frac{e^{K|x-x_0|}-1}{K}$

次回は積分定数について書く予定だが数式を打ち込むのに疲れてきたので飛ばすかもしれない。

2015-05-09

微分方程式メモ (2)

予告した通り今回は解の一意性について書く。まだ1日も経っていないがしばらく数式を打ち込んでいられる余裕も無さそうだから早めに投稿した。あくまでもメモであって、人に見せることは考えずに書いているので注意。

逐次近似法により $y(x_0)=y_0$ を満足する $dy/dx=f(x,y)$ の解 $y(x)$ を得た。しかし、 $dy/dx=f(x,y)$ の解の一意性についてまだ確かめていない。同じ初期条件を満たす別の解がある可能性が残っているのだ。
前回のメモで設定した以下の2つの条件の下、一意性を証明する。
条件1:函数 $f(x,y)$ は実数値で、 $|x-x_0|≦a$ 、 $|y-y_0|≦b$ $(a,b＞0)$ で定義される $(x,y)$ 平面の領域 $D$ で連続である。
条件2: $f(x,y)$ は $D$ で $y$ に関してリプシッツ条件を満たす。つまり、正定数 $K$ が存在し $D$ の任意の点の組 $(x_1,y_1)$ 、 $(x_2,y_2)$ に対し
$|f(x_1,y_1)-f(x_2,y_2)|≦K|y_1-y_2|$
が成り立つ。
[証明]
$z(x)$ を $z(x_0)=y_0$ 、 $z(x)=y_0+\int_{x_0}^{x}f(t,z(t))dt$ を満たす $dy/dx=f(x,y)$ の解とする。
条件2より、
$|y(x)-z(x)|=\left|y_0+\int_{x_0}^{x}f(t,y(t))dt-y_0-\int_{x_0}^{x}f(t,z(x))dt\right|$
$=\left|\int_{x_0}^{x}f(t,y(t))dt-\int_{x_0}^{x}f(t,z(x))dt\right|$ $=\left|\int_{x_0}^{x}f(t,y(t))dt-f(t,z(x))dt\right|$
$≦\left|\int_{x_0}^{x}K|y(t)-z(t)|dt\right|=K\left|\int_{x_0}^{x}|y(t)-z(t)|dt\right|$
ここで $N=sup_{|x-x_0|≦h}|y(x)-z(x)|$ とおくと、 $|x-x_0|≦h$ で
$|y(x)-z(x)|≦KN|x-x_0|$
この不等式で $|y(x)-z(x)|≦K\left|\int_{x_0}^{x}|y(t)-z(t)|dt\right|$ の右辺の $|y(t)-z(t)|$ を評価すると、
$|y(x)-z(x)|≦K\left|\int_{x_0}^{x}|y(t)-z(t)|dt\right|≦K\left|\int_{x_0}^{x}KN|t-x_0| dt\right|$
$=K^{2}N\left|\int_{x_0}^{x}|t-x_0|dt\right|=K^{2}N\frac{{|x-x_0|}^{2}}{2}≦\frac{N(Kh)^{2}}{2}$
さて、 $|y(x)-z(x)|≦\frac{N(K|x-x_0|)^{n-1}}{(n-1)!}$ であるとすれば
$|y(x)-z(x)|≦K\left|\int_{x_0}^{x}|y(t)-z(t)|dt\right|≦K\left|\int_{x_0}^{x}\frac{N(K|t-x_0|)^{n-1}}{(n-1)!}dt\right|$
$=K^{n}N\left|\int_{x_0}^{x}\frac{{|t-x_0|}^{n-1}}{(n-1)!}dt\right|≦K^{n}N\frac{{|x-x_0|}^{n}}{n!}$
$=\frac{N{(K|x-x_0|)}^{n}}{n!}≦\frac{N{(Kh)}^{n}}{n!}$
よって任意の $m$ に対し $|y(x)-z(x)|≦\frac{N{(Kh)}^{m}}{m!}$ が成立。
右辺は $x$ の選び方に依らないので $N≦\frac{N{(Kh)}^{m}}{m!}$ が言える。しかし $\frac{{(Kh)}^{m}}{m!}$ は $m$ を大きくしていくと $1$ より真に小さくなり、 $N=0$ でなければこの不等式は成り立たない。
$|y(x)-z(x)|≦N=0$ より $y(x)=z(x)$ であるから、解は一意的である。証明終。

逐次近似法の手順を説明するため、ひとつ例を見てみよう。
初期条件 $y(0)=1$ の下で、 $\frac{dy}{dx}=y(x)$ を解く。前回のメモと同じようにして函数列 ${(y_n(x))}_{n∈ \bf N}$ を定義する:
$y_0(x)=y_0=1$
$y_1(x)=y_0+\int_{x_0}^{x}f(t,y_0)dt=1+\int_{0}^{x}1dt=1+x$
$y_2(x)=y_0+\int_{x_0}^{x}f(t,y_1(t))dt=1+\int_{0}^{x}1+tdt=1+x+\frac{x^2}{2}$
$y_3(x)=y_0+\int_{x_0}^{x}f(t,y_2(t))dt=1+\int_{0}^{x}1+t+\frac{t^2}{2}dt=1+x+\frac{x^2}{2}+\frac{x^3}{6}$
…
以上から $y_n(x)=\sum_{k=0}^{n}\frac{x^k}{k!}$ と予想できる。 $n=1$ の時は成立している。
$y_{n-1}(x)=\sum_{k=0}^{n-1}\frac{x^k}{k!}$ と仮定すると、
$y_n(x)=1+\int_{0}^{x}\sum_{k=0}^{n-1}\frac{t^k}{k!}dt=1+\sum_{k=0}^{n-1}\int_{0}^{x}\frac{t^k}{k!}dt$
$=1+\sum_{k=1}^{n}\int_{0}^{x}\frac{t^{k-1}}{(k-1)!}dt=1+\sum_{k=1}^{n}\frac{x^k}{k!}=\sum_{k=0}^{n}\frac{x^k}{k!}$
従って、先程の予想は正しい。
微分方程式 $dy/dx=y(x)$ の解 $\lim_{n \to \infty}y_n(x)=y(x)$ は、
$\lim_{n \to \infty}y_n(x)=\lim_{n \to \infty}\sum_{k=0}^{n}\frac{x^k}{k!}=\sum_{k=0}^{\infty}\frac{x^k}{k!}$
こうして $y(x)=exp(x):=e^x$ が導かれた。

次回は $n$ 次近似解 $y_n(x)$ の誤差評価について書く予定。

2015-05-09

微分方程式メモ (1)

微分方程式についてのメモ。参考文献は Lectures on differential and integral equations (Kosaku Yoshida) である。TeXコマンドはよくわからないので見づらいのは許して欲しい。
さて、1階常微分方程式はふつう $F(x,y,dy/dx)=0$ の形で書かれる。以下、これが $\frac{dy}{dx}$ について解くことができ、 $\frac{dy}{dx} =f(x,y)$ の形で書かれる場合について考える。 $\frac{dy}{dx} =f(x)$ というのが最も単純な場合であるが、この解は $f(x)$ が連続な変域において
$y(x) =\int_{x_0}^{x}f(t) dt + C$
で与えられる。積分定数 $C$ は $x=x_0$ における $y(x)$ の値により定まる。すなわち $y=y(x_0)=C$ である。つまり、 $y(x_0)=y_0$ を満たす $\frac{dy}{dx} =f(x)$ の解は
$y(x) = y_0+\int_{x_0}^{x}f(t) dt$
で与えられる。条件 $y(x_0)=y_0$ は初期条件と呼ばれる。
$y(x_0)=y_0$ を満たす微分方程式 $\frac{dy}{dx} =f(x,y)$ の一般解を見つけたいのであるが、この問題を形式化するため、 $f(x,y)$ に関して2つの条件を設定する。
条件1:函数 $f(x,y)$ は実数値で、 $|x-x_0|≦a$ 、 $|y-y_0|≦b$ $(a,b＞0)$ で定義される $(x,y)$ 平面の領域 $D$ で連続である。
条件2: $f(x,y)$ は $D$ で $y$ に関してリプシッツ条件を満たす。つまり、正定数 $K$ が存在し $D$ の任意の点の組 $(x_1,y_1)$ 、 $(x_2,y_2)$ に対し
$|f(x_1,y_1)-f(x_2,y_2)|≦K|y_1-y_2|$
が成り立つ。
ここで、 $f(x,y)$ が $D$ において連続な偏導関数 $\frac{∂f(x,y)}{∂y}$ を持つ時、 $f(x,y)$ が条件2を満たすことを見てみよう。
$\left| \frac{∂f(x,y)}{∂y} \right|$ は連続で、 $D$ が有界閉集合であることより $\left| \frac{∂f(x,y)}{∂y} \right|$ は有界。よって、 $K= sup_{(x,y)∈D}\left| \frac{∂f(x,y)}{∂y} \right|$ とおける。ここで、 $x$ を固定し、 $f_{(x)}(y)=f(x,y)$ とすると、 $\frac{df_{(x)}(y)}{dy}= \frac{∂f(x,y)}{∂y}$ である。 $(x,y_1)、(x,y_2)∈D$ に対し平均値の定理より、ある $\theta∈(y_1,y_2)$ が存在し、
$\frac{f_{(x)}(y_1)-f_{(x)}(y_2)}{y_1-y_2}=\left( \frac{df_{(x)}}{dy} \right) (\theta)$
が成立。従って、
$\frac{f(x,y_1)-f(x,y_2)}{y_1-y_2}= \frac{∂f}{∂y} (x,\theta)$
両辺に絶対値を付けて
$\left| \frac{f(x,y_1)-f(x,y_2)}{y_1-y_2} \right| = \left| \frac{∂f}{∂y} (x,\theta) \right|$
$K= sup_{(x,y)∈D}\left| \frac{∂f(x,y)}{∂y} \right|$ より、
$\left| \frac{f(x,y_1)-f(x,y_2)}{y_1-y_2} \right| ≦ K$
故に、 $|f(x,y_1)-f(x,y_2)| ≦ K|y_1-y_2|$ が導かれる。 $x$ は任意であるから、 $f(x,y)$ はリプシッツ条件を満たす。これで条件2の重要性がわかったかと思われる。
条件1より、 $|f(x,y)|$ は有界閉領域 $D$ 上で連続であるから、 $|f(x,y)|$ は $D$ 上有界である。よって、 $M= sup_{(x,y)∈D} |f(x,y)|$ とおける。 $h=min\{a,\frac{b}{M}}\$ とすると、区間 $|x-x_0|≦h$ 上で函数列 ${(y_{n}(x))}_{n∈\bf N}$ を以下のように定義することができる:
$y_0(x)=y_0$
$y_1(x)=y_0+\int_{x_0}^{x}f(t,y_0(t)) dt$
$y_2(x)=y_0+\int_{x_0}^{x}f(t,y_1(t)) dt$
…
$y_n(x)=y_0+\int_{x_0}^{x}f(t,y_{n-1}(t)) dt$

定理: ${(y_n(x))}_{n∈\bf N}$ は区間 $|x-x_0|≦h$ において一様収束し、その極限 $y(x)$ は初期条件 $y(x_0)=y_0$ を満たす $dy/dx=f(x,y)$ の解である。
[証明]
$M= sup_{(x,y)∈D} |f(x,y)|＜ \infty$ と $h=min\{a,b/M\}$ より、 $|x-x_0|≦h$ で、 $k=1,2,…,n$ に対し
$|y_k(x)-y_0|=\left| \int_{x_0}^{x}f(t,y_{k-1}(t)) dt \right|≦|x-x_0|sup_{(x,y)∈D}|f(x,y)|≦hM$
また、 $h$ の定義より $hM≦b$ がわかる。
従って、 $k=1,2,…,n$ に対し $|y_k(x)-y_0|≦hM≦b$ が成立。
ここで、リプシッツ条件を用いる。
$|f(t,y_k(t))-f(t,y_{k-1}(t))| ≦ K|y_k(t)-y_{k-1}(t)|$
左辺の絶対値は外せる。
$f(t,y_k(t))-f(t,y_{k-1}(t)) ≦ K|y_k(t)-y_{k-1}(t)|$
両辺 $t$ について積分すると、
$\int_{x_0}^{x}f(t,y_k(t))-f(t,y_{k-1}(t)) dt ≦ \int_{x_0}^{x}K|y_k(t)-y_{k-1}(t)| dt$
$\int_{x_0}^{x}f(t,y_k(t)) dt - \int_{x_0}^{x}f(t,y_{k-1}(t)) dt ≦ K \int_{x_0}^{x}|y_k(t)-y_{k-1}(t)| dt$
$\int_{x_0}^{x}f(t,y_k(t)) dt + y_0 - y_0 - \int_{x_0}^{x}f(t,y_{k-1}(t)) dt ≦ K \int_{x_0}^{x}|y_k(t)-y_{k-1}(t)| dt$
$y_{k+1}(x)-y_{k}(x) ≦ K \int_{x_0}^{x}|y_k(t)-y_{k-1}(t)| dt$
両辺絶対値を付けて、
$|y_{k+1}(x)-y_{k}(x)| ≦ K \left| \int_{x_0}^{x}|y_k(t)-y_{k-1}(t)| dt \right|$
この不等式を認めれば、 $k=1,2,…,n$ で
$|y_{k}(x)-y_{k-1}(x)| ≦ \frac{b{(K|x-x_0|)}^{k-1}}{(k-1)!}$
が導かれる。 $k=1$ の時は明らかであるから、 $k=n$ で上の不等式が成り立つと仮定すると、 $k=n+1$ でも
$|y_{n+1}(x)-y_{n}(x)| ≦ \frac{b{(K|x-x_0|)}^{n}}{n!}$
が成り立つ。よって数学的帰納法より任意の $k$ についてこれが成り立つ。細かい証明はダルいので演習問題とする。
この時、 $m＞n$ で
$|y_m(x)-y_n(x)| ≦ \sum_{k=n}^{m-1}|y_{k+1}(x)-y_k(x)|$
$≦\sum_{k=n}^{m-1} \frac{b{(K|x-x_0|)}^{k}}{k!}≦\sum_{k=n}^{m-1} \frac{b{(Kh)}^{k}}{k!}$
が得られる。
$|y_m(x)-y_n(x)| ≦\sum_{k=n}^{m-1} \frac{b{(Kh)}^{k}}{k!}$ の右辺を $n→\infty$ とすると、 ${(y_n(x))}_{n∈\bf N}$ は区間 $|x-x_0|≦h$ で函数 $y(x)$ に一様収束することがわかる。一様収束することから、 $y(x)$ は連続かつ初期条件 $y(x_0)=y_0$ を満たす。
$y(x)$ が $dy/dx=f(x,y)$ の解であることを示すために、この命題を用いる。
命題:函数列 ${(y_n(x))}_{n∈\bf N}$ が一様収束し、 $y_n(x)$ が区間 $|x-x_0|≦h$ で連続ならば、以下が成立。
$\lim_{n \to \infty} \int_{x_0}^{x}y_n(t) dt = \int_{x_0}^{x} \lim_{n \to \infty}y_n(t) dt$
これもダルいので証明しない。
これを認めれば、 $\lim_{n \to \infty}y_n(x)=y(x)$ は $y_0+ \int_{x_0}^{x}f(t,y(t))dt$ に一致する:
$\lim_{n \to \infty}y_n(x)=y_0+\lim_{n \to \infty}\int_{x_0}^{x}f(t,y_n(t))dt$
$=y_0+\int_{x_0}^{x}\lim_{n \to \infty}f(t,y_n(t))dt=y_0+\int_{x_0}^{x}f(t,y(t))dt$
被積分函数 $f(t,y(t))$ は連続なので、 $y(x)$ は微分可能である。
よって、導函数 $dy/dx$ は
$\frac{dy}{dx}=\frac{d}{dx}y_0+\frac{d}{dx}\int_{x_0}^{x}f(t,y(t))dt=f(x,y(x))$
となり、 $y(x)$ が $dy/dx=f(x,y)$ の解であることがわかる。証明終。

これ以上やるとページがクソ重くなりそうなので一旦終了。次回は解の一意性について書く。